
The Gillespie Papers Project has been established as a private www.viewzone.com archive to discuss and evaluate the unpublished papers and notes of Dr. Rollin Gillespie. Dr. Gillespie's unique genius in the understanding of harmonics resulted in numerous inventions and advances in science. In his last work he attempts to describe the sun and planets as being a "multi-body solution to the angular momentum problem" that allows a new look at gravity and electrical attraction. Actual quotes from notes in blue blocks. Your comments and discussion is encouraged. Submit comments "here".
|
|
Additional Notes: Solution Of The Multi Body Gravitational Problem There are two classes of multibody gravitational problems. The solar system is typical of one class, and the Hercules globular star cluster is typical of the other. The spread sheet display in the preceding section is in actual fact a general solution for all members of the first class, in which all orbits are confined to the approximate plane or the equator of a relatively massive dominant body, and in which there are three more bodies. If the low, whole, odd-number, harmonic ratio of each adjacent pair of minor bodies is specified, there is one and only one solution for each system. Highly inclined orbital planes are excluded from the solution, and are probably impossible for the reason that they would quickly be forced into alignment with the equatorial plane. Low whole number harmonics correspond to the lowest energy states of the system, but the lowest. 2/1 and 4/1, are forbidden by the repetitive alignment of tidal forces in a single direction.  View of the Solar System. There is one and only one solution that can be shown by a simple consideration of the solar system. As stated above in the section, "The Angular Momentum Problem," the angular momentum of the system is overwhelmingly concentrated in the planets. Although an expansion of the orbits reduces both the rotational rate and the angular momentum of the central body, there comes a point when there is no more angular momentum in the central body than the amount necessary to maintain its angular rate of rotation, equal to twice the sum of the angular rates of revolution of the planets. At the same time, there is nothing to stop the expansion of the orbits until that point is reached.
 View of Hercules Galaxy - a global cluster. The globular star cluster is governed by a different mechanism. The Hercules cluster is described by Robert Burnham, Jr., in his "Celestial Handbook," Vol II (Dover, 1978). Although in a telescope the cluster appears to be crowded with stars, he describes a model in which a million grains of sand are distributed throughout a spherical volume some 300 miles in diameter. Each grain would be 0.03 inch in diameter, and separated from the next nearest grain by a distance of three miles. The dynamics of the cluster would be defined by the random motions of individual stars, prevented from escape by the gravitational field of the cluster. Collisions would be extremely far apart in time. |
|
What is the Bode Titus Law?
The Bode-Titus law is an empirical rule giving the approximate distances of planets from the Sun. It was first announced in 1766 by the German astronomer Johann Daniel Titius and only popularized, from 1772, by his fellow countryman Johann Elert Bode. The rule may be given as follows: Write down the sequence 0, 3, 6, 12, 24, etc. To each number add 4. Divide each result by 10. Of the first seven answers (0.4, 0.7, 1.0, 1.6, 2.8, 5.2, 10.0), six closely approximate the distances from the Sun, in astronomical units (AU's, the distance between the Earth and the Sun), of the six planets known when Titius devised the rule: Mercury, Venus, Earth, Mars, Jupiter, and Saturn. 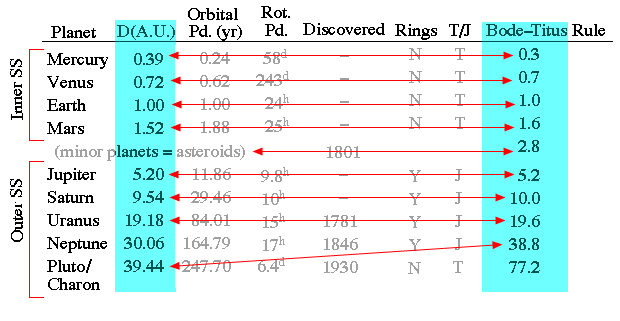 At about 2.8 AU's from the Sun, between Mars and Jupiter, the asteroids (sometimes called minor planets) were later discovered. The rule also holds for the seventh planet, Uranus, which lies at about 19 A.U. Bode's law fails for the eighth planet, Neptune. However, Pluto/Charon, the ninth planet from the Sun, is at a distance (39 AU's) roughly equal to that given by the rule for the eighth planet. |