
The Gillespie Papers Project has been established as a private www.viewzone.com archive to discuss and evaluate the unpublished papers and notes of Dr. Rollin Gillespie. Dr. Gillespie's unique genius in the understanding of harmonics resulted in numerous inventions and advances in science. In his last work he attempts to describe the sun and planets as being a "multi-body solution to the angular momentum problem" that allows a new look at gravity and electrical attraction. Actual quotes from notes in blue blocks. Your comments and discussion is encouraged. Submit comments "here".
|
The Strong Force
Sunspots
The period of revolution of Jupiter is 11.861773 Earth years. The average cycle of sunspots is given as 11.120412 years. During one cycle the zones in which the spots occur begin at high latitudes and end in low latitudes. The magnetic fields of the spots are said to be reversed each cycle. The cycles are erratic in the abundance of spots, and in duration, and sometimes a sequence of cycles vanishes altogether. At times the phase of a cycle is displaced from the end of one cycle to the beginning of the next. However, they do tend to progress gradually in intensity and duration, and then start a new progression. There is abundant evidence that variations in weather, and in such phenomena as auroras and radio transmission, are correlated with sunspot activity. There is some reason to believe that the electrical activity of the human brain can be modulated by sunspot activity. It may be that terrestrial phenomena are not so much influenced by sunspots themselves, as by other types of solar activity associated with sunspot cycles. However, the observations of sunspots have been recorded in greater detail, and since much earlier times, than have such phenomena as solar flares, and are thus available for correlation studies.
The ratio of the period of Jupiter's revolution around the Sun to the length of cycle of sunspot activity is suggestive.
11.861773 / 11.120412 = 1.066667
Compare this number with the Sun-Jupiter barycenter distance from the center of the Sun, namely 1.068 solar radii.
|

|
Turbulence which emerge on the surface of the Sun as spots, being closely related to the period of Jupiter, must form at the bottom of the Jupiter rotation zone in the Sun. This would be at a distance from the axis of 0.586 the solar radius, the distance of the Saturn barycenter. The cylinder of that radius intersects the surface of the Sun at 35.9 degrees, which just happens to be the latitude, both North and South, at which sunspots first appear at the beginning of each cycle. Any given spot is carried with the surrounding fluid at the speed of the fluid. However, the spacing of spots is not a function of angular rotation rate, but of the transport of the center of the Sun, and therefore the Sun as a whole, through inertial space.
The Sun's axis is tilted 7.25 degrees from the normal to the plane of Earth's orbit. In the 11.861773 year revolution of the Jupiter-Sun barycenter around the Sun, the relative positions of the tilted Sun resemble the equinoxes and solstices on Earth. Because of the great mass of the Sun, the gyroscopic forced produced by Jupiter do not cause it to precess rapidly, but they can supply the energy to create the eddies which appear on the surface of the Sun as spots and flares. The precessional force would be least at the "solar equinoxes," and greater at the "solar solstices." There would be a tendency for the rotating cylinder "sleeves" in the Sun to align themselves with the common axis of the planetary orbits, which would create confusion as the Sun tends to maintain the sleeves concentric with its own axis. However, the problem could likely be solved in a computer, projecting thousands of years into the past and into the future.
The calculation of the changing configuration of barycenters in the Sun presents the same problem, and for the same reasons, as the calculations of any multibody gravitational system. Until now, there has been no general mathematical solution. Yet nature finds solutions. There are occasional three-body star systems among the millions of binary stars. The solar system in a multi-body solution that must have been repeated trillions of times in the universe.
(next section: More About Mercury And Planet Z) |
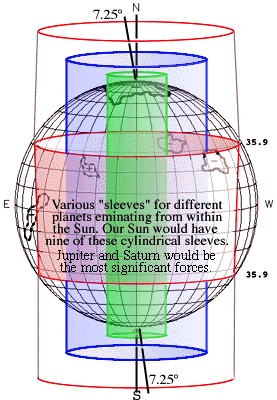 The center of the Sun is 1.068 solar radii from the Jupiter-Sun barycenter, and therefore must travel through inertial space 1.068 times as fast as it would if the barycenter were on the Sun's surface. The Sun as a whole must travel through inertial space at the same speed. This would reduce the sunspot cycle from 11.861773 years to 11.120412 years. The variability of the sunspot cycle can be attributed to the added effects of the other planets, and to the continual changing of the planetary alignments.
The center of the Sun is 1.068 solar radii from the Jupiter-Sun barycenter, and therefore must travel through inertial space 1.068 times as fast as it would if the barycenter were on the Sun's surface. The Sun as a whole must travel through inertial space at the same speed. This would reduce the sunspot cycle from 11.861773 years to 11.120412 years. The variability of the sunspot cycle can be attributed to the added effects of the other planets, and to the continual changing of the planetary alignments.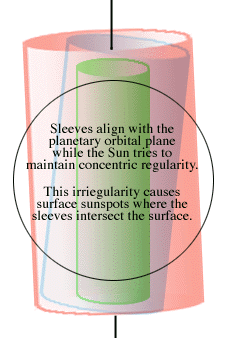 The rotating cylindrical sleeves would be subjected to large pressures in the Sun's interior, but at their intersection with the surface the pressure would be reduced, and centrifugal force would tend to make them expand. Expansion could not be toward the poles of the Sun, and therefore would have to be toward the equator. The circulation pattern induced by the expansions of nine sleeves, each tending to follow the motions of its associated planet barycenter would be complex, but the overall trend would have to be toward the equator. This may account for the gradual drift of sunspot activity toward the equator during the course of each cycle.
The rotating cylindrical sleeves would be subjected to large pressures in the Sun's interior, but at their intersection with the surface the pressure would be reduced, and centrifugal force would tend to make them expand. Expansion could not be toward the poles of the Sun, and therefore would have to be toward the equator. The circulation pattern induced by the expansions of nine sleeves, each tending to follow the motions of its associated planet barycenter would be complex, but the overall trend would have to be toward the equator. This may account for the gradual drift of sunspot activity toward the equator during the course of each cycle.